Toy Neural Network Classifies Orientation of Line

Play with the toy neural network animation featured above. It takes as input a simple toy image of a "line" which may be oriented any of four ways: horizontally, vertically, diagonally, or fill the entire image. Click on one of the line images under "SELECT DATA" in the upper left and watch as the network correctly classifies the orientation of the line.

Artificial neural networks are abstractly inspired by the basic computational units of the brain, neurons. State of the art solutions to AI problems including image recognition, natural language processing, simulating human creativity in the arts, and outperforming humans in complex board games are backed by artificial neural networks. Instead of being hard-encoded with rules, artificial neural networks learn a task from training examples. For instance in visual pattern recognition, to recognize images of a particular object, like the number “9”, programs are confronted with the difficulty of considerable variability: flourishes in handwriting style, lighting of the surrounding context, changes in orientation and size. To write precise rules would necessitate limitless exceptions. Artificial neural networks approach the problem by learning to infer rules from training examples. Here we will outline the mechanics of a simple neural network and illustrate the property of hierarchical feature detection.

PERCEPTRON
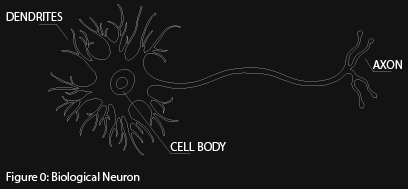
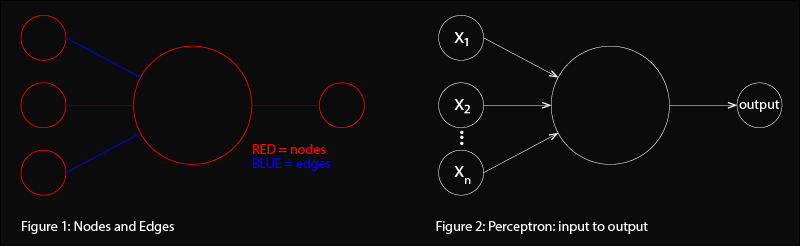
The biological inspiration operates by communicating via electrical impulses. Each biological neuron consists of a cell body (which generates electrical signals), dendrites (which receive signals), and an axon (which sends signals) (figure 0). Simply, a neuron is electrically excited by an input at its dendrites. That electrical input comes from another neuron or numerous neurons. If the input is strong enough, then the neuron is "activated" and fires its own electrical output down its axon. That axon is perhaps connected to the dendrites of other neurons. In this way electrical signals are transmitted across networks of neurons. In artificial neural networks, neurons are represented by nodes (red circles) and connections to other neurons are represented by edges (blue lines) (figure 1). The simplest and earliest model is the perceptron, which also is the fundamental building block of more complex neural networks. A perceptron takes binary inputs, \( x_1, x_2,… x_n \) and outputs a single binary output (figure 2).
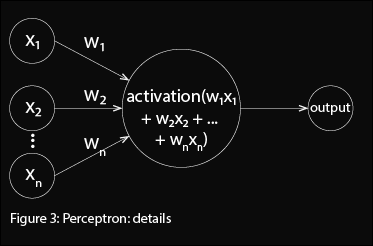How is the output computed? Each input is multiplied by its respective weight, \( w_1, w_2, ... w_n \). The weight determines the relative influence of each input (the greater the weight, the greater the influence on the output). Then every input multiplied by its weight is summed together: \( w_{1} x_{1} + w_{2} x_{2} + \cdots + w_{n} x_{n} = \sum_{i=1}^{n} w_{i} x_{i} \). The perceptron's output is determined by whether this weighted sum of all its inputs, \( \sum_{i=1}^{n} w_{i} x_{i} \), exceeds some threshold value:

$$ output =\left\{ \begin{array}{c l} 0 \qquad \text{ if } \sum_{i} w_i x_i \leq threshold \\ 1 \qquad \text{ if } \sum_{i} w_i x_i > threshold \end{array}\right. $$ If we think of 0 as "off" and 1 and "on" then this threshold function effectively determines whether the perceptron is turned on or off. This function is aptly named the activation function since it determines if the perceptron is activated (switched on) or not. Activation is like overcoming a barrier or filling a cup. Only when the cup overflows or the barrier is crossed will the switch be activated. In biology, different neurons need different levels of input stimulation before they will fire an electrical output. Some neurons need very little whereas others need a lot to be activated.

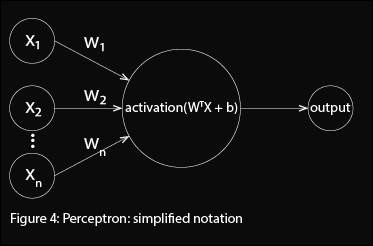Simplifying, if we consider all the weights and inputs as vectors: $$ W = \begin{bmatrix} w_1 \\ w_2 \\ ... \\ w_n \end{bmatrix}, \hspace{10mm} X = \begin{bmatrix} x_1 \\ x_2 \\ ... \\ x_n \end{bmatrix} $$ then the transpose of the weight matrix W multiplied by the input matrix X is the same as the weighted sum: \( W^{T}X = [w_1 \hspace{2mm} w_2 \cdots w_n] \begin{bmatrix} x_1 \\ x_2 \\ ... \\ x_n \end{bmatrix} \) \(= w_{1} x_{1} + w_{2} x_{2} + \cdots + w_{n} x_{n} = \sum_{i=1}^{n} w_{i} x_{i}. \)
Furthermore if we let the bias = -threshold. Then the equivalent rule for the perceptron becomes (figure 4): $$ output =\left\{ \begin{array}{c l} 0 \qquad \text{ if } W^{T}X + b \leq 0\\ 1 \qquad \text{ if } W^{T}X + b > 0 \end{array}\right. $$
This formulation of the perceptron is the most commonly used in the literature.

ACTIVATION FUNCTIONS
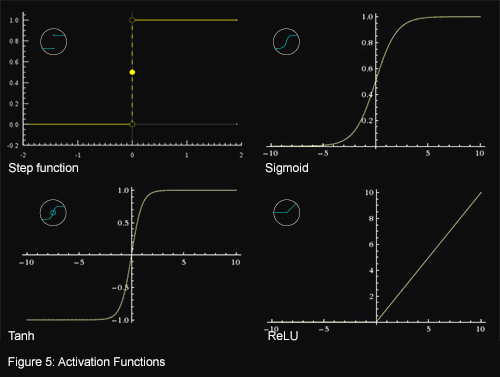
Notice that \( W^T X + b\) is a linear function. If this were all to neural networks, then they would not be able to do more than linear regression. Activation functions, \( \Phi \), also serve the critical role of introducing nonlinearity into the network. $$ output = \Phi (W^{T}X + b) $$ $$= activation (W^{T}X + b) $$ The most frequently used activation functions are the sigmoid, tanh and reLU. How much does the introduction of non-linearity enable a neural network to represent? As is proven, neural networks with at least one hidden layer are universal approximators, which means they can represent any continuous function (see Approximation by Superpositions of a Sigmoidal Function and a visual proof). In diagrams, each activation function is represented by one of the following symbols:

See figure 5 to determine which symbol corresponds to which activation function.


MULTILAYER NETWORK
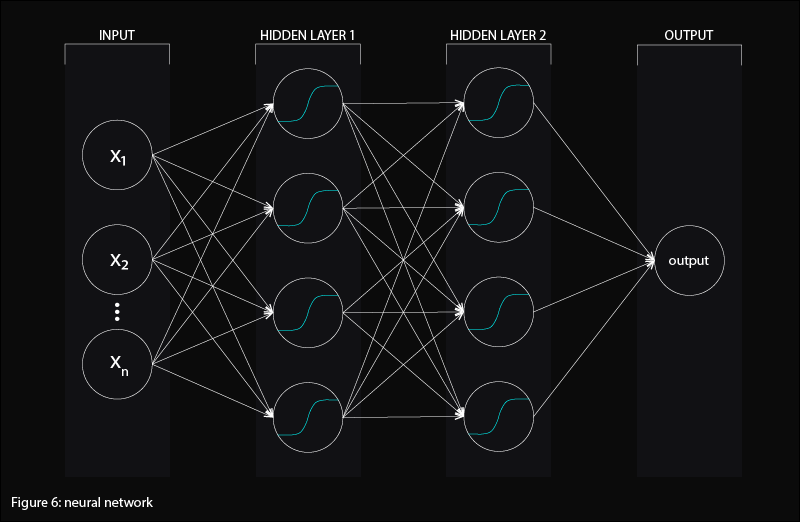
The perceptron is a single layer neural network in which inputs are directly summed and activated to produce an output. Deep neural networks have a multilayer structure where neurons are organized into distinct layers. Two adjacent layers may have any combination of connections between them (with a full set of connections being common), but no two neurons in the same layer are connected (figure 6).
This layered organization may enable hierarchies of feature detectors. The toy visual recognition animation featured above exemplifies this hierarchical grouping of learning more complex composite features in deeper layers. Earlier layers detect simpler features. The first hidden layer recognizes single pixels. The second hidden layer recognizes composites of two pixels. The third recognizes composites of 4 pixels and the fourth layer recognizes the negation of layer three. This deep architecture wherein lower layers recognize simpler features which feed into higher layers that detect more complex features (such as a progression from line edge orientations, to contours, to fully developed outlines) is a breakthrough in visual recognition: Convolutional Deep Belief Networks for Scalable Unsupervised Learning of Hierarchical Representations.

To illustrate these concepts, let's look at a concrete example and tease apart the animation that opens this article. Here it is diagrammed (figure 7): 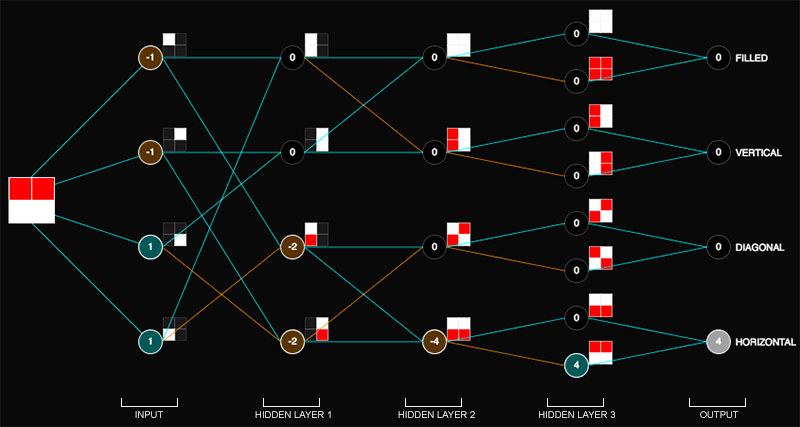Figure 7: Diagram of opening animation

The input is a toy "image" that is made of 4 pixels. The input images feature a simple line in red which can be oriented any of the following ways: horizontally , vertically , diagonally , or no line . The task of the neural network is, given an input image of a line, to correctly classify the orientation of that line. This is a highly simplified example of visual pattern recognition.

In the input layer of the neural network (figure 7), 4 nodes examine the 4 pixels: one node is associated with each pixel of the input image. The 4-square next to each node indicates which pixel each node examines. For instance, this 4-square next to the first node means the first node holds the data for the upper left pixel. If in the input image the pixel is red, the node registers a value of -1. If the pixel is white, the node registers 1. So in this representation, red is the negation of white, or another way to see it is that the line is the opposite of the background.

Hidden Layer 1
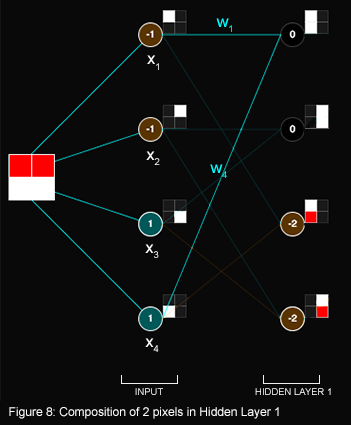
Hidden Layer 1 exemplifies the first instance of hierarchical feature representation, meaning deeper layers combine simpler earlier layers to recognize more complex features. Whereas the input layer only recognized one pixel at a time, Hidden Layer 1 combines the single pixels from the input into combinations of 2-pixels (figure 8). The edges that feed into the nodes of Hidden Layer 1 determine which two pixels are combined. For instance there are edges from the first and last node of the input layer feeding into the first node of Hidden Layer 1 which means the upper left pixel and the lower left pixels are combined: + = (figure 8).

A cyan edge means the edge has a weight of +1.
An orange edge means the edge has a weight of -1.

Let's see how we get the value of 0 in the first node of Hidden Layer 1: \( x_1 \)\( w_1 \) + \(x_4\)\(w_4\) = (-1)(1) + (1)(1) = 0, where \( x_1 \) is the first node and \( x_4 \) is the fourth/last node of the input layer.




Hidden Layer 2
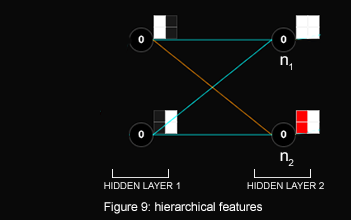
Let's see how the first node of Hidden Layer 2, \( n_1 \), is computed (figure 9):
()(1) + ()(1) =

\( n_2 \):
()(-1) + ()(1) =
Recall that we defined the negation of white to be red,
therefore: ()(-1) =

Activation Functions
For hidden layers 1 and 2, the activation function lets the signal pass through so long as the value is not zero. Zero effectively switches off the node and the signal dies. Otherwise any other value keeps the switch on. Figure 10 shows where zero flips off the switch. Hidden layer 3 uses the reLU activation function, which turns all negative values into zero and leaves positive values unchanged.

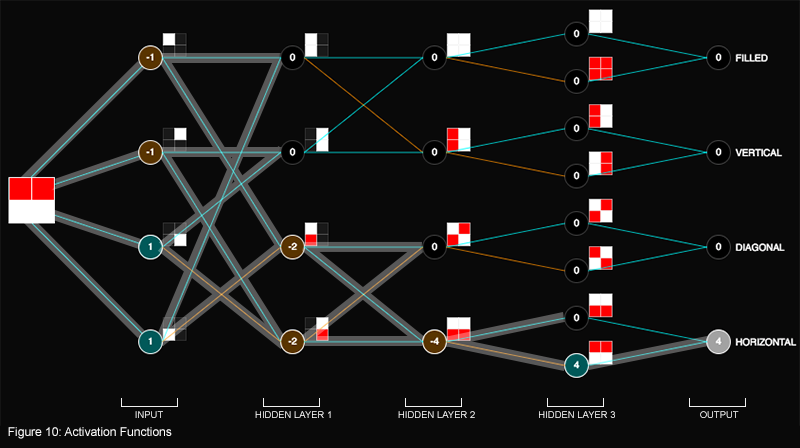
This toy neural network illustrates the basic mechanics of neural networks (activation functions acting on weighted summation of inputs) and hierarchical feature representations in which deeper layers in the network allow for compositions of features developed in earlier layers that hence enables more sophisticated processing.


Citations
1. CS231n Convolutional Neural Networks for Visual Recognition
2. Neural Networks and Deep Learning
3. Convolutional Deep Belief Networks for Scalable Unsupervised Learning of Hierarchical Representations
4. Approximation by Superpositions of a Sigmoidal Function
5. A visual proof that neural nets can compute any function
6. How Deep Neural Networks Work